SVM Formulación del problema desde un punto de vista 'real'👑
Durante este post usaremos un conjunto de datos un tanto peculiar;
\[\pi = \{(x_i, y_i) , x_i \in R^p, y_i \in \{Austrias, Borbones\} \}^m_{i=1}\]Como representantes de la dinastía borbónica he escogido a mí trío favorito: Carlos IV, su esposa María Luisa de Parma y Manuel Godoy. Sí, Godoy no es ningún borbón, pero existen razonables dudas sobre la parte que le ocupó a Carlos en los 14 hijos de María Luisa de Parma y si a esto le añadimos el razonable parecido de estos con Godoy junto a la promiscuidad y desatención de la pobre María Luisa por parte de su marido…
Como representantes de la dinastía de los austrias tenemos a Juana I la Loca, Carlos II el Hechizado y el príncipe don Carlos (primogénito de Felipe II). Creo que estos tres personajes representan a la perfección la demencia y los frutos de la consanguinidad que caracterizaron a la dinastía de los austrias.
Respecto al poco conocido Carlos, creo que merece algunas palabras. El pobre nunca llegó a ser rey, murió a manos de su malvado padre (Felipe II) o esa es la versión que se nos ha intentado vender por parte de los británicos. En realidad, Carlos era un sádico con graves problemas mentales. Sus problemas se manifestaron bien pronto, cuando era bebé. En aquella época era habitual que la reina no amamantase a sus hijos sino que lo hiciesen las nodrizas, bien, a nuestro amiguito Carlos no le convencía ninguna teta ya que mordía los pezones de sus amas hasta llagarlos y estas terminaban muriendo debido a la sepsis provocada por las heridas. Intentaron que una cabra amamantase a Carlos pero él era más listo que sus amas; él quería carne humana. Su vida no duró mucho, murió a los 23 años tras un encierro (por voluntad de su malvado padre) que acrecentó su locura.

Un dataset $D = \{(x_i, y_i) , x_i \in R^p, y_i \in {-1, 1} \}^m_{i=1}$ linealmente separable puede clasificarse usando varios hiperplanos diferentes. Un modelo de clasificación como el perceptrón encontrará miles de hiperplanos diferentes. Las SVM en vez de encontrar un hiperplano cualquiera, encuentran el señor hiperplano, el que mejor separa entre los datos.
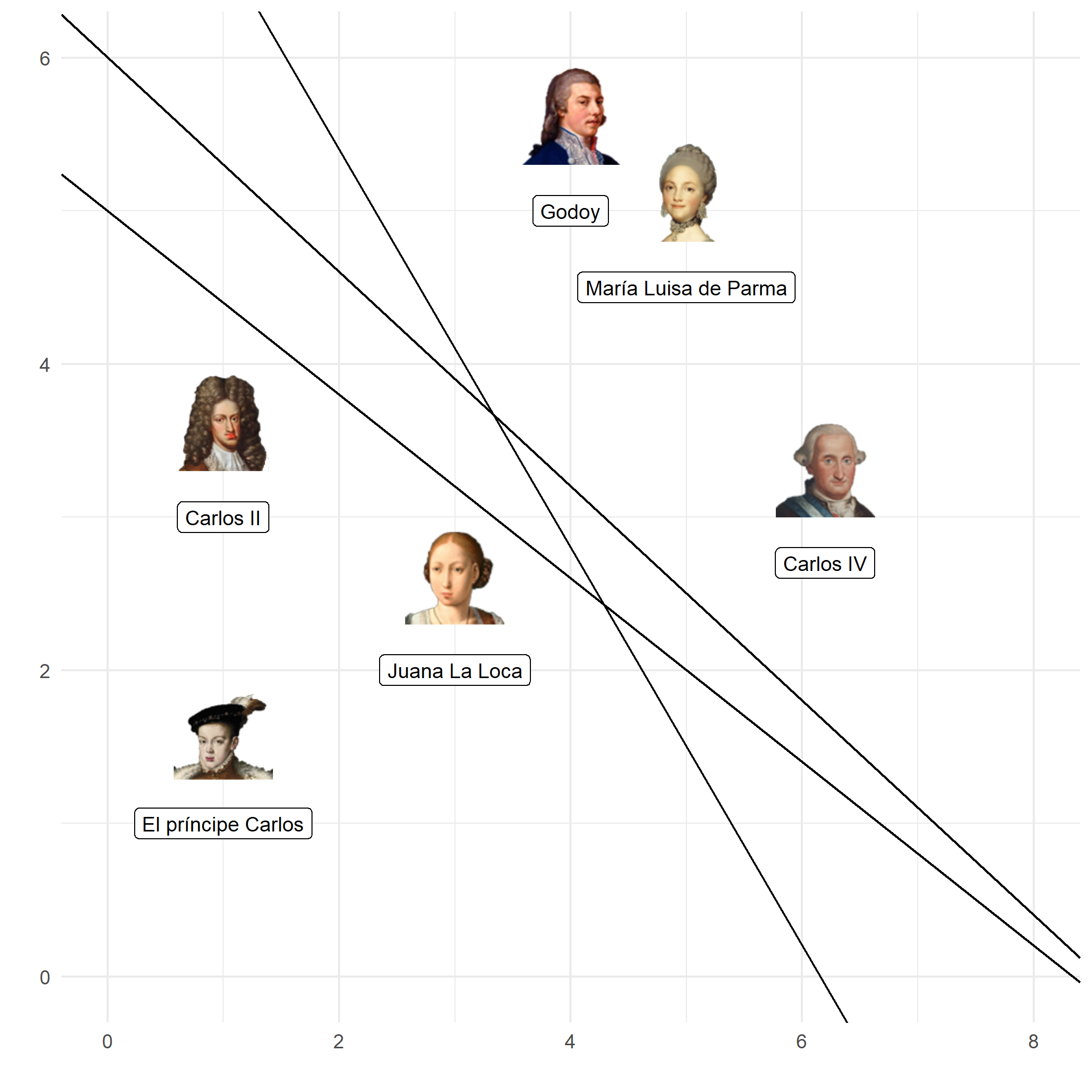

¿Cómo comparar dos hiperplanos?
Para encontrar el señor hiperplano primero debemos saber cómo comparar dos hiperplanos. Dada una observación $(x_{Juana}, y)$ y un hiperplano, si Juana se encuentra en el plano, se satisface la ecuación del plano; $wx_{Juana} + b = 0$. ¿Pero qué ocurre si no se está en el plano? Definamos un hiperplano con $w = (-0.6, -1)$ y $b=7$.
- Para Juana I La Loca (5, 4); $wx_{Juana} + b = 0$ como ya habíamos comentado
- Para María Tudor (3,2); $wx_{María} + b = 3.2$
- Para Carlos V de Alemania (1.5, 0.5); $wx_{Carlos} + b = 5.6$
- Para Pepe Botella (tan querido por el pueblo español), que es un dato atípico en nuestro dataset (y en la historia de España); (7, 6); $wx_{Jose} + b = -3.2$

Como acabamos de ver, si nuestro personaje se sitúa por encima del hiperplano el valor es negativo y positivo en caso contrario. Por ello, para el problema de clasificación inicial podemos usar la siguiente regla para clasificar en una clase u otra:
\[Austria \;\;\; \rightarrow \;\;\; si \;\;\; wx_i + b > 0\] \[Borbón \;\;\; \rightarrow \;\;\; si \;\;\; wx_i + b \leq 0\]Además, según se alejan nuestros monarcas del hiperplano, la ecuación de este asigna un valor cada vez mayor. Entonces, podemos calcular el valor $\beta = wx + b$ para saber lo lejos que se encuentra una observación del hiperplano. El mejor hiperplano será aquel que tenga las observaciones tan alejadas como sea posible. Definimos $B$ como el menor valor de todos los $\beta$ de nuestro dataset. Si queremos escoger entre dos hiperplanos, escogeremos el que tenga un mayor $B$.
\[B = \underset{i=1,...,m}{\text{min}} \beta_i\]Problemas con esta aproximación
Si decidiéramos comparar dos hiperplanos según $B$ tendríamos un problema, escoger el $\beta_i$ mínimo no funciona para las observaciones en la parte negativa (donde se encuentra Pepe Botella).
Siempre querremos que el $\beta_i$ mínimo sea el del punto más cercano al hiperplano. Entre dos observaciones con $\beta_1 = -5$ y $\beta_2=-1$, escogeríamos $\beta_1$ porque $\beta_1 < \beta_2$, pero, en realidad, $\beta_1$ está más lejos del hiperplano que $\beta_2$. Una forma de solucionar este problema es considerar el valor absoluto de $\beta_i$.
\[B = \underset{i=1,...,m}{\text{min}} | \beta_i |\]Más problemas
Vamos a trabajar con una variable respuesta que tomará el valor +1 si la observación pertenece a los Borbones y -1 si pertenece a los Austrias (no eran muy positivos).
Calcular $B$ nos ayuda a escoger el hiperplano, pero usando solo $B$ podríamos escoger el hiperplano erróneo. En la siguiente gráfica vemos que en el hiperplano de color rojo las clases se separan bien (la clase negativa de los Austrias está por encima de la recta y la clase positiva por debajo), pero en el segundo hiperplano (negro) las clases están mal clasificadas. Sin embargo, ambos hiperplanos tienen un $B = 2$.

La solución en este caso pasa por considerar el valor de la observación en la variable respuesta (-1 o 1). Definimos el valor $f_i = y_i \beta_i = y_i (wx_i + b)$. $f_i$ tomará un valor positivo si la observación está bien clasificada y negativo si no lo está. Así, dado un dataset podemos calcular $F$ que será el menor $f_i$ del dataset. Si nuestro hiperplano no es el correcto, $F$ tomará un valor negativo. Por tanto, al igual que con $B$, seleccionaremos el hiperplano que mayor $F$ tenga.
\[F = \underset{i=1,...,m}{\text{min}} f_i = \underset{i=1,...,m}{\text{min}} y_i(wx_i + b)\]El valor $f_i$ se conoce como functional margin of an observation y el valor $F$ como functional margin of the dataset.
Escalado
Houston, tenemos un (otro) problema; $f_i$ no es invariante a la escala. Dado el vector $w_1 = (2, 1)$ y $b_1 = 5$ si multiplicamos ambos por 10 tenemos $\rightarrow$ $w_2=(20,10)$ y $b_2 = 50$. Si calculamos $F$ con $w_2$ obtenemos un valor 10 veces mayor que con $w_1$, lo que nos lleva a afirmar que dado cualquier hiperplano, siempre podremos encontrar otro con un $F$ mayor reescalando $b$ y $w$. Para que esto no sea un problema, usaremos el vector unitario de $w$, dividiendo $w$ por su norma euclídea, también lo haremos con $b$. A este nuevo valor lo designaremos con la letra $\gamma_i$ que se conoce como geometric margin of an observation. La ventaja de $\gamma_i$ es que siempre nos devuelve el mismo valor sin importar la escala de $b$ o $w$.
\[\gamma_i = y_i(\frac{w}{||w||}x_i + \frac{b}{||w||})\]Definimos $M$ como el menor $\gamma_i$ del conjunto de datos, y al igual que antes, seleccionaremos el hiperplano que mayor $M$ tenga.
\[M = \underset{i=1,...,m}{\text{min}} \gamma_i = \underset{i=1,...,m}{\text{min}} y_i(\frac{w}{||w||}x_i + \frac{b}{||w||})\]Margen geométrico ?
A $\gamma_i$ se le llama margen geométrico porque mide la distancia entre una observación $x_i$ y el hiperplano. Para entender por qué el margen geométrico es equivalente a la distancia entre una observación y el hiperplano tomemos a Carlos IV ($x_{Carlos}$) como referente (aunque Carlos IV y referente podría ser un ejemplo de antítesis).

El punto $x’$ es la proyección ortogonal de $x_{Carlos}$ en el hiperplano. El vector $k$ tiene la misma dirección que el vector $w$ que define el hiperplano, comparten el mismo vector unitario; $\frac{w}{\lVert w \rVert}$. La norma de $k$ es la distancia entre el hiperplano y la observación; $d$. Por tanto, $k = d \frac{w}{\lVert w \rVert}$. Bien, si nos fijamos veremos que $x’$ es la resta de $x$ y $k$, o sea, $x’ = x - k = x - d \frac{w}{\lVert w \rVert}$ . Como $x’$ se encuentra en el hiperplano, debe satisfacer su ecuación;
\[wx' + b = 0\] \[w(x - d \frac{w}{||w||})+b = 0\] \[wx - d \frac{ww}{||w||}+b = 0\] \[wx - d \frac{||w||^2}{||w||}+b = 0\] \[wx - d ||w|| + b = 0\] \[d = \frac{wx + b}{||w||}\] \[d = \frac{w}{||w||}x + \frac{b}{||w||}\]Y si nos damos cuenta, la expresión de $d$ es la misma que la de $\gamma_i$ $\rightarrow$ el margen geométrico es la distancia entre una observación $x$ y su proyección en el hiperplano.
Hiperplano óptimo
Como hemos visto, para encontrar el hiperplano que nos ofrezca un mayor margen debemos encontrar el hiperplano que maximice $M$. Podemos escribirlo de la siguiente forma;
\[\underset{w, b}{\text{max}} \; M\] \[s.t \;\; \gamma_i \geq M, i= 1, ..., m\]Hay una relación entre $M$ y $F$ como ya hemos visto $\rightarrow$ $M = \frac{F}{\lVert w \rVert}$. Podemos reescribir el problema como;
\[\underset{w, b}{\text{max}} \; \frac{F}{\lVert w \rVert}\] \[s.t \;\; \frac{f_i}{\lVert w \rVert} \geq \frac{F}{\lVert w \rVert}, i= 1, ..., m\]Eliminando $\lVert w \rVert$ de la inecuación tenemos que;
\[\underset{w, b}{\text{max}} \; \frac{F}{\lVert w \rVert}\] \[s.t \;\; f_i \geq F, i= 1, ..., m\]Intentamos maximizar el margen geométrico, por tanto, la escala de $w$ y $b$ no importan. Es decir, podemos variar $w$ y $b$ tanto como queramos que $\gamma_i$ no se verá afectado por ello. Por tanto, escalamos $w$ y $b$ de forma que $F=1$.
\[\underset{w, b}{\text{max}} \; \frac{1}{\lVert w \rVert}\] \[s.t \;\; f_i \geq 1, i= 1, ..., m\]Este problema es equivalente a;
\[\underset{w, b}{\text{min}} \; \lVert w \rVert\] \[s.t \;\; y_i(wx_i + b)\geq 1, i= 1, ..., m\]Sin embargo, se suele cambiar la función objetivo y en vez de considerar la norma euclídea se eleva esta al cuadrado para que desaparezca la raíz. Además y por conveniencia se multiplica por $\frac{1}{2}$. Así finalmente llegamos a la conocida función a minimizar de las máquinas de soporte vectorial.
\[\underset{w, b}{\text{min}} \; \frac{1}{2} \lVert w \rVert^2\] \[s.t \;\; y_i(wx_i + b) - 1 \geq 0, i= 1, ..., m\]En resumen, hemos asumido que existen algunos hiperplanos que son mejores que otros. Para encontrar el hiperplano óptimo hemos llegado a la conclusión de que se debe maximizar el margen geométrico; $M$. El mejor hiperplano será aquel que tenga un mayor $M$. Al final, hemos concluido que el vector $w$ del hiperplano óptimo se encuentra minimizando la norma de $w$.
Referencias
- Data Science y redes complejas (Eloy Vicente Cestero y Alfonso Mateos Caballero)
- Support Vector Machines Succinctly (Alexandre Kowalczyk)